Здравствуйте, дорогие читатели! Как и было обещано в прошлой статье, сегодня я пишу о НОД. Естественно, у многих сразу появился вопрос, что это такое. Объясняю. НОД расшифровывается как Наибольший Общий Делитель. То есть разговор ведется о наибольшем делителе для двух чисел одновременно. Приведу пример: имеется два числа — 24 и 9. Самое большое число, на которое они оба делятся без остатка — это число 3, которое и будет являться НОД. Также, когда говорят об наибольшем общем делителе, упоминают о загадочном для некоторых алгоритме Евклида. На самом деле все гораздо проще. Дело в том, что алгоритм Евклида — это такой алгоритм, который как раз таки и позволяет найти НОД. Но следует запомнить, что алгоритм рассчитан на действия с двумя целыми неотрицательными числами. Это важный момент, который нельзя упускать.

Теперь посмотрим на принцип алгоритма, в котором используется деление с остатком.

Расписываю по пунктам алгоритм Евклида:

1. Берем два целых неотрицательных числа
   2. Сравниваем их и находим остаток от деления большего числа на меньшее.
   3. Если остаток равен 0, то это значит, что делитель и есть НОД (Выходим из цикла).
   4. Если же в результате деления мы получили не 0 в остатке, то большему числу присваиваем остаток, который получили в пункте 2 (заменяем большее число на остаток от деления).
   5. Возвращаемся к пункту 2.

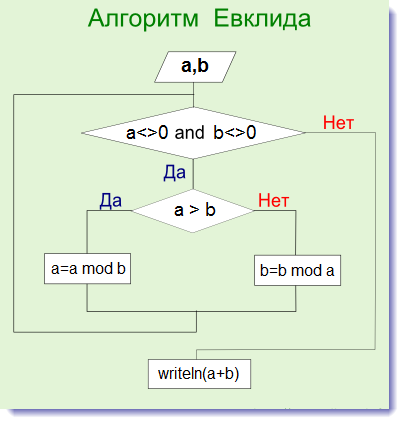
Для тех, кому все еще не понятно, приведу блок-схему алгоритма на примере двух чисел, пусть это будут числа a и b.

Вернемся к нашему примеру с числами 24 и 9. Опишу пошагово, как, используя алгоритм Евклида, мы приходим к тому, что НОД в этом случае равно 3

1. Берем числа m = 24 и n = 9.
2. m > n {m=24,n=9}
   3. m := m mod n
   4. m > n {m=6,n=3}
   7. m := m mod n
   8. т.к m = 0 выходим из цикла. НОД равен n = 3

Ну а сейчас алгоритм Евклида в паскале.

var
m, n: integer;
begin
Writeln(‘Введите два числа’);
Readln(m, n);
{старт цикла }
repeat
if m > n then m := m Mod n
else n := n Mod m;
until (m = 0) Or (n = 0);
{если или m или n в процессе хода цикла стал равен 0 ,то цикл заканчивается }
writeln(‘НОД = ‘, m + n); {так как мы знаем ,что одно из чисел равно нулю ,а другое НОД , то мы выводим сумму этих чисел}

end.